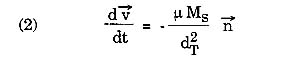|
 |
SUR L'INTERPRETATION DES EXPERIENCES DE MICHELSON
Aucun vent d'éther de 30 km/s, mais un vent d'éther de 8 km/s
par Maurice Allais - Mars 2004
Max Planck - Initiations à la Physique, 1925
" Tout le travail et le zèle du chercheur ne pourraient lui apparaître que comme une tentative vaine et sans espoir s'il n'y avait, de temps en temps, certains faits de nature à lui prouver irréfutablement que le va-et vient de ses démarches tâtonnantes lui a permis finalement de faire un pas de plus vers la vérité".
Auguste Fresnel - De la lumière, 1822
" Quand une hypothèse est vraie, elle doit nous conduire à la découverte des rapports numériques qui lient entre eux les faits les plus éloignés".
Henri Poincaré - Science et Méthode, 1908
" Si un résultat nouveau a du prix, c'est quand, en reliant des éléments ... paraissant étrangers les uns aux autres, il introduit subitement l'ordre là où régnait l'apparence du désordre. Il nous permet alors de voir d'un coup d'oeil chacun de ces éléments et la place qu'il occupe dans l'ensemble".
RESUME
Le présent mémoire présente
quelques compléments essentiels à mes précédentes publications.
1.- L'analyse des azimuts du pendule paraconique
et des visées sur mires et sur collimateurs démontre l'existence de composantes
lunisolaires correspondant à une influence de la Lune.
2.-
La distribution des Planètes et des Satellites des Planètes est caractérisée
par des régularités très remarquables.
3.-
Pour chaque Planète, et chaque Satellite des Planètes, la vitesse est égale à
la vitesse de l'Ether environnant. En particulier la Terre et l'Ether ont le même
mouvement autour du Soleil.
4.-
Tout se passe comme si la vitesse de la Lune autour de la Terre engendrait une
vitesse de l'Ether à la surface de la Terre qui se révèle égale à la vitesse moyenne
de 8 km/s correspondant aux hodographes déduits des observations de Miller.
De cette égalité résulte une confirmation très
remarquable de la validité à la fois des observations de Miller et de la formulation
des effets interférométriques de Michelson.
5.-
Au total il y a un vent d'éther à la surface de la Terre (Aether Drift) mais
ce vent d'éther n'est pas de 30 km / sec. comme admis a priori par Michelson. Il
est de 8 km / sec. correspondant à la vitesse de l'Ether à la surface de la Terre
engendrée par la vitesse de la Lune autour de la Terre.
6.- Ainsi, un vent d'éther de 8 km/s à la surface de la Terre est engendré par le mouvement de la Lune
Il en résulte une extraordinaire vérification de la validité à la fois des observations de Miller et des formulations interférométriques de Michelson.
____________________________________
COMPOSANTES LUNISOLAIRES DES AZIMUTS DU
PENDULE PARACONIQUE ET DES VISEES SUR MIRES ET SUR COLLIMATEURS
L'analyse harmonique des azimuts du pendule paraconique et des visées sur
mires et sur collimateurs démontre l'existence de composantes lunisolaires diurnes de 24h
50mn et de composantes lunaires mensuelles sidérales de 27,322 jours correspondant à une
influence marquée de la Lune, totalement inexplicable dans le cadre des théories
actuelles. (Voir Expériences de Maurice Allais de
1952 à 1960 )
LA DISTRIBUTION
DES PLANETES
ET DES
SATELLITES DES
PLANETES
FORMULATION A*.
CAS n = 0
Modèle considéré
Dans mon Mémoire sur la distribution des Planètes
et des Satellites des Planètes ( Voir Etude de décembre 2003 )
j'ai indiqué qu'il était possible de représenter la distribution des Planètes autour
du Soleil, et des Satellites des Planètes autour de leur Astre central, par les relations
(1) log d *n’ = A* n' + e n’
(2) d *n = d n
/ ra
(3) n' = n +
na*
na* = entier positif
où d n représente
la distance du satellite d'indice n à l'Astre central et ra le rayon de
l'Astre central.
Le
nombre entier n désigne le numéro d'ordre du satellite.
Le bord de l'astre central est défini par les
relations
(4)
d *a = 1
log d *a = 0 n’a= 0
(5)
n’a = n + na* na = - na*
Ajustements
Tout Satellite correspond à une valeur entière de n', mais à toute valeur de n' on peut faire correspondre soit un satellite effectif, soit un satellite fictif.
En particulier à la valeur n' = 0 du bord du Soleil on peut faire correspondre un
Satellite fictif.
L’EGALITE DE LA VITESSE DES
PLANETES - ET DES SATELLITES DES PLANETES - ET DE LA VITESSE DE L'ETHER ENVIRONNANT -
LA GENERALISATION DE
LA TROISIEME
LOI DE KEPLER AU CAS DES VITESSES DE
L'ETHER
Le cas de la Terre et des Planètes
1.- Dans le cas de la Terre j'ai démontré que la
vitesse de l'Ether environnant est égale à la vitesse de la Terre. Le même
calcul reste valable pour toute Planète.
2.- Dans son principe le même calcul reste
encore valable pour tout Satellite d'une Planète.
3.- Il résulte de là que pour toute Planète la
vitesse de l'Ether environnant est égale à la vitesse de la Planète.
Pour le système solaire la Troisième Loi de
Kepler s'écrit
|
où d représente la distance d'une Planète au Soleil, T sa période de
révolution, MS la masse du Soleil, et µ le coefficient de la gravitation
universelle.
En première approximation on a
|
(8) v
2 d = µ MS
et par suite pour deux Planètes P1 et
P2
(9)
v1 2
d1 = v22
d2
ou encore
|
LA VITESSE DE L'ETHER
A LA
SURFACE DE
LA TERRE INDUITE PAR
LE MOUVEMENT DE
LA LUNE
1.- Il résulte de ce qui précède et tout
particulièrement de la relation (10) ci-dessus que l'on a
|
où v représente la vitesse de l'Ether au voisinage de la Terre engendrée
par le mouvement de Lune, V représente la vitesse de la Lune (égale à la vitesse de
l'Ether environnant la Lune), D la distance de la Lune à la Terre,et R le rayon de la
Terre.
2.- On a
|
où T représente la période de révolution
sidérale de la Lune.
 |
On
a ainsi d'après (12)
 |
et
par suite d'après (11)
Soit
| (16) | v = 7,9460 km/sec
|
D'après mon article de La Jaune et la Rouge on a pour la valeur moyenne v des valeurs calculées
(17) |
v = 8,02 km/sec
|
l'écart est donc d'environ 0,5 %.
Signification
des calculs
On ne saurait trop souligner ce qu'implique
l'égalité approchée
- de la valeur
moyenne
déduite
de l'analyse des observations de Miller, où à aucun moment le mouvement de la Lune n'est
considéré.
- et de la vitesse
correspondant à la vitesse de l'Ether engendrée
à la surface de la Terre par le mouvement de la Lune.
- En fait, et fondamentalement, il s'agit bien dans les deux cas d'un
même phénomène, un vent d'éther.
On a donc bien un vent d'éther, mais
son origine est totalement différente de ce que l'on attendait a priori, savoir
l'influence du mouvement de la Terre au sein d'un Ether que l'on supposait immobile.
- Dans cette perspective, les calculs qui précèdent et leur résultat final démontrent :
1.- La cohérence et la validité des
hypothèses et des calculs effectués dans la
présente Note.
2.- Une remarquable vérification de la
validité à la fois des observations de Miller et des formules interférométriques de
Michelson.
.
APPENDICE
EGALITE DE LA VITESSE
DE LA
TERRE
ET DE L'ETHER
ENVIRONNANT
Le texte qui
suit est extrait du livre de Maurice Allais, 1997 : « L’anisotropie de
l’Espace », p. 423-424, note (8)
_____________________________________________________________________
II est facile de vérifier que les données de
l'observation sont tout à fait compatibles avec l'hypothèse d'un fluide, l'Ether,
animé d'un mouvement de rotation de 30 km/sec, autour du Soleil.
Pour un tel fluide on a en effet
|
(R.
Bricard, Calcul vectoriel, Chapitre VII B, Hydrodynamique, Armand Colin, 1929, p. 162).
| Comme il s'agit d'un mouvement permanent on a |
|
Si l'Ether tourne avec la Terre autour du Soleil son accélération
est la même que pour la Terre et on a en un point M de la trajectoire de la Terre et en
première approximation :
|
|
|||
|
Enfin on a
Or, en unités CGS (Allais, 1997, L'anisotropie de l'Espace, p. 124, note 15, et p. 119, note 5)
|
La relation (1) s'écrit donc
(7)
-
0,5930 = 0,5956 - 1,1912 + e
L'écart e = + 0,0046 résulte des
approximations faites.
On vérifie ainsi que l'Ether peut être considéré comme animé
du même mouvement que la Terre autour du Soleil.
Si on désigne par a , b , c les valeurs absolues
de ses trois ternies la relation (7) s'écrit en première approximation
(8) - a = b - c
avec
(9)
a = b
c = 2 b
La relation a = b correspond au fait que pour la
Terre la force d'attraction a est compensée par la force centrifuge b.
REFERENCES
Albert A. MICHELSON
1881 The relative
motion of earth and the luminiferous aether
The American Journal of Science : Third
Series, Vol. XXII,1881, Art. XXI, pp. 120-129.
1887 The relative motion of the earth and the
luminiferous aether
The American Journal of Science : Third
Series, Vol. XXTV,1887, Art. XXXVI, pp. 333-345.
1925
The Effect of thé Earth's Rotation on the
Velocity of Light
The Astrophysical Journal,
April 1925.
1933
The
Ether-Drif Experiments and thé Détermination of the
Absolute Motion of the Earth
Reviews of Modem Physics, Vol. 5, July 1933,
n° 3, pp. 203-242.
Maurice
ALLAIS
1997 L'Anisotropie de l'Espace Editions Clément Juglar, 760 pages
.
2003 Des régularités
extraordinaires et irréfragables dans les observations interférométriques de Dayton C.
Miller 1925-1926, L'effondrement radical et définitif de la Théorie de la
relativité
Fusion, mai-juin 2003, pp. 38-47. La Jaune et la Rouge, Octobre 2003, pp.79-88.
2003 Sur la distribution
des Planètes et des Satellites des Planètes, 29 janvier 2004, 72 pages.
2003
Sur la signification de mon article de La Jaune et la Rouge d'octobre 2003 au
regard de
la
genèse et du développement de la Théorie de la Relativité, 29 janvier 2004, 11 pages.